先に結論だけ書くと「桃鉄で狙って好きな出目を出すこと」は出来ません。しかし、ちょっとだけ「桃鉄で有利になること」は狙って出来ます。
必要なものは算数の知識とそれをゲームに活かす考え方だけ。
世間では桃鉄こと桃太郎電鉄ブームということで、色々な方がプレイしてるのをよく見かけました。しかし、カードや物件の知識はあるのにサイコロの出目については完全に運まかせでプレイしてる人が多い印象です。
ですが、ちょっとだけ算数の知識があれば、有利になれるんですよね。
というわけで、サイコロの出目についてちょっと書いてみようかと思います。
これからするおはなしは、確率の操作をする裏技やチートとかではなく、単純に算数的なおはなしです。
※サイコロの確率がおかしいと思ってこの記事を読みに来ている人も結構居たので、そちらについてはちょっと別記事で書きました。【桃鉄のサイコロがおかしいと思ってしまう理由の考察】
サイコロの出目は均等に出るわけじゃない?
桃鉄では、サイコロの出目は均等に出ません。カードがあるから。
サイコロの出目は1~6までが均等に1/6ずつでしょ!と思われるでしょうが、もちろんそのとおりです。それは正しい認識でしょう。
ところが、今書いているのは「桃鉄でのサイコロの話」です。
そして、桃鉄にはあるんですよね、一度に振れるサイコロの数を増やすカードが何種類も。
2個にする急行カード、3個にする特急カードからもっと増やすカードまで色々と。
これらのカードが実に曲者で、直感でプレイングミスをしてしまう原因になってます。
具体的にどういうことなのかは次へ。
2個以上のサイコロの出目の合計は均等に出ない
サイコロが2個以上になると、出目の合計は均等に出てくれません。
理由は簡単で、数学的にそうなっているから。
結論だけ言われても分からないかもしれませんので、例を挙げて説明して行きましょう。
まずは急行カードでサイコロを2つにしたパターンで見ていきます。
当たり前の話ですが、合計が2になるパターンは1+1のパターンのみ。
片方でも2~6の目が出た時点で合計が2になることはなくなります。
合計が12になるパターンも同じで、6+6のパターンしかありません。
ところが合計が7になるパターンなら、片方で1~6のどれが出ていてももう片方で6~1になれば合計7になるわけです。1と6、2と5,3と4、4と3、5と2、6と1。
つまり、6パターンあることになります。
2個のサイコロの合計が2や12になるパターンよりも7になるパターンの方が圧倒的に多いですね。
これを実際に計算して表にしてみるとこんな感じです。
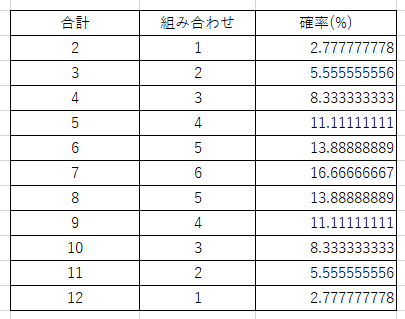
サイコロ1つで一番大きい6を出すよりも、2個で合計6を出す方が出やすそうと直感的に思ってしまう人も割と居るとは思います。
1個だと一番大きい数字である6、2個だとだいたい真ん中の6ですからね。
ですが、サイコロが1つのままだと1/6で16.67%、2つだと13.89%で急行カードを使ったほうが出る確率が下がります。
特急カードを使って3個にした場合も見てみましょう。
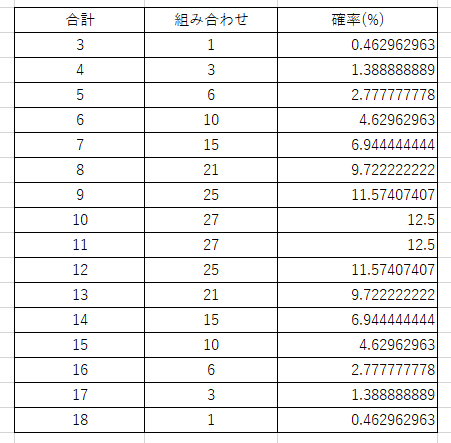
さきほどと同様にど真ん中の10と11が出やすくなっています。しかし、出目が3~18になったぶん一番出やすい10・11でも12.5%まで下がってます。
実はこれ、サイコロ1個の出目を3.5として計算すると何個に増やしても「合計値はいくつが一番出やすいか」がわかります。
例えば4個だと3.5×4が14なので「14が一番出やすい」と計算可能。
というわけで、2個以上のサイコロの出目は均等に出ないということが理解してもらえたと思います。
そうしたら次へ行きましょう。理屈から実践編です。
実戦でこの確率を利用するために気をつけること
今回は桃鉄の話ですので、注意点がもちろんあります。
桃鉄のマップは(一部の場所を除くと)一直線のマップではありません。
なので遠回りという手段が可能です。
さきほど「残り6マスの場合はサイコロは1個の方が出やすい」と書きましたが「最短では6マスだけど遠回りをすれば9マスでもいける」場合はそれぞれの出る確率を足すことになります。
「6の出る確率13.89%」に「9の出る確率11.11%」を足すので25%ほどになるため、急行カードを使うほうが通常1個で6が出る確率の16.67%よりも有利になる、という計算です。
このように、遠回りが可能な場所を目指す場合は意外と計算が面倒だったりもします。
逆に、空路や海路などでルートが一本しか無い離島などでは遠回りが不可能なため単純に計算可能ですね。
確率を知っていれば知らない人よりはちょっとだけ有利な程度
ここまで書いたとおり遠回りも考慮して厳密に計算すると滅茶苦茶大変なので、普通の人の脳みそではあまり役に立たない内容だったように思えます。
しかし、カードを使うタイミングを計る材料には使えます。
例えば、ルートが2本あって10マスでも11マスでもゴールに入れるような場所があったときに「特急カードは10と11が一番出やすい」と知ってたとしましょう。
そこで「いま特急カードを使えば12.5%+12.5%で最低でも25%(更に大きい数字で遠回り可能な場合も出る確率を+するのでそちらも考慮するとさらに増えます)でゴール出来る」とわかります。
このように考えれば、カードを使うかどうかの判断の材料として利用できますよね。
他にも、10マス目と11マス目のどちらも良い物件のあるマスや良い効果のマスと分かっているケースなんかが良い例です。
これも一番出やすい出目が両方とも良いマスなので、特急カードを使うチャンスのはず。25%でそのどちらかにたどり着けます。
今挙げた例のように、出目の確率を知っていれば急行系カードを使うかどうかの判断材料のひとつになるわけです。
まとめ
ということで、知っていればサイコロの目を狙い放題!!!みたいな感じにはまったくなりません。
ですが、何も知らずに居るよりは良いタイミングで急行系カードを使えるようになります。
という、かんたんな算数のおはなしでした。
中盤以降は周遊カードが貯まりますし、後半はロイヤルEXやリニア周遊を複数枚抱えて(周遊カードの残り回数回復マスに寄りながら)常にサイコロ5個以上で好きなマスに移動しまくるゲームになるんですけどね。
それでも序盤や周遊を溜め込む余裕がない内はちょっとだけ役に立つでしょう。
※サイコロの確率がおかしいと思ってこの記事を読みに来ている人も結構居たので、そちらについてはちょっと別記事で書きました。【桃鉄のサイコロがおかしいと思ってしまう理由の考察】
おまけ:今回解説したような、ゲームに使えそうな算数や数学の話に興味が出た人はこちらをどうぞ。
普通の「確率・統計」本は最低でも高校数学をマスターしていることが前提のものが多いですが、こちらは初心者向けの入門本なので割と気軽に読める一冊です。
ゲームに使える確率や統計学に本格的に興味が出てきたら、今度は専門の本を読んで、自分が好きなゲームに使えないか考えてみるのも楽しいと思います。

