土木や外構工事のときに使う専用の機械は高精度のものだと数十万円します。中古で探しても中々のお値段になってしまうので、DIYでは手が出ません。
というわけで、今回は高級な機材を使わずに精度の良い直角を出せる方法を紹介しようと思います。
最低限必要なものはメジャー（スケール）と杭やピン、「３・４・５」という数字くらい。
※庭づくりや土木・外構で使うためのもので、10m進んだときに誤差が3mm以下のような超精密な墨出しが求められている場合は使えません。それはもうトランシットという高級機材の出番です。
直角を作るカギは「３・４・５」の３つの数字
急に３・４・５と言われても何のことかわからない方もいるかもしれませんが、実は過去に習っているはずです。それがこの図。
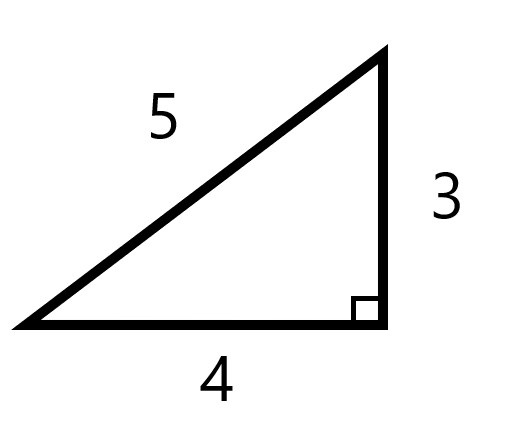
はい、教科書に出てきたであろう直角三角形です。30°・60°・90°の「1:2:√3」などは今でも覚えているかも知れません。それと同じタイプで数字がもっともキリの良い直角三角形のバージョンです。
この三角形を使えば数m単位の大きさでもそれなりの精度で直角が出せてしまいます。主に土木工事の方や型枠大工さんなんかが知っていたりします。（彼らはきちんと機材を用意出来ているので普段から使うことはありませんが）
詳しい説明は省きますが、三平方の定理（ピタゴラスの定理）のお陰で直角を挟んで３と４を取れば、残る斜辺は必ず５になります。これを逆に使って直角を作ってしまおうというのが今回の手順。
せっかく数学で学んだものなので、庭造り・外構のDIYにも使ってしまいましょう。知識は使わないともったいないですから。
実際に３・４・５を使って大きな直角を出す手順
まずは基準にしたい点とラインを決めます。これは自分が基準にしたい点とラインなので自由に。実際に線を引いても良いですし、引かなくても可能です。
基準点と基準ラインが決まったら、基準点をAとし、基準ラインの上で基準点から4mの場所に点Bを取りましょう。
※4mと3mのどちらでも可能ですが、墨出しをする場合は直角の長い方を先にすることの方が多いです。理由を説明すると細かいので今回は割愛します。「直角を扱う場合は長い方を先」と覚えておけば大抵の場合で正解です。
基準点Aと点Bが取れたら、今度は自分が「大体直角かな？」と思うラインを出し、点Aから3m測って点C（仮）を作ります。
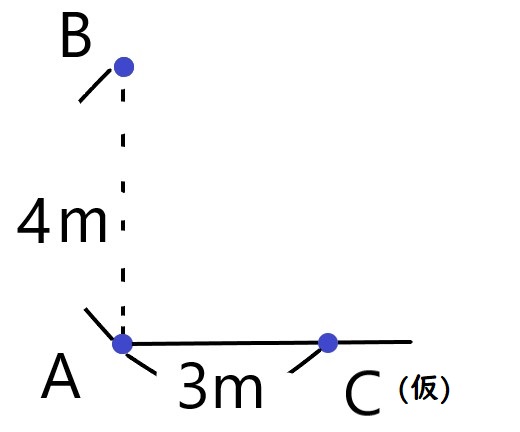
ここでさきほどの三角形を使います。
もし点Aの部分の角が完璧に直角なら、点Bと点C（仮）を結んだ距離は5mぴったりになるはずです。
というわけで、点Bから点C(仮）までの距離を測ります。
もしこの距離が5mより大きければ直角より開きすぎてますし、逆に5mより小さければ直角より小さくなっています。その数字を見ながら調整して、ぴったりになる場所に本物の点Cを取ります。
点Aとの距離が3mで点Bとの距離が5mになる完璧な点Cが取れたら、基準線ABと線ACのところの角が念願の直角になっているはずです。これで完了。
ですが、確認の意味でAB間ももう一度測ってみることをおすすめします。作業中に点Bが動いてしまっていないかの確認のために。
DIY流の工夫でさらにかんたんに直角が出せるのがこの方法
点の部分には杭やピンを刺しておけば良いですし、言ってしまえば距離を取るのはメジャー（巻き尺）である必要すらありません。
さきほどのやり方の例ですと、３ｍの部分はどうせ長さは固定なので余っている木材などに穴を空けて点Aのピンに通し、そこから3mの部分に印をしておけば「位置は動かないけど角度は自在に変わる3mの定規」になります。
あとはこの定規の角度を変えつつBC間の距離が5mぴったりになるように調整すればOK。実はこの即席定規でやってることってコンパスと同じなんですね。
「コンパスと同じなら別に紐や糸でもできるんじゃ？」と思うかも知れませんが、素人がやるのはNGです。
紐や糸は思っているよりも伸び縮みします。なんなら安い布系のメジャーも伸びます。なので、外構のように大きな墨出しをする場合はできる限り伸びないものを使ってやりましょう。プロが数十メートル単位で使う巻き尺はスチールなどで伸びにくい材質になっています。こんな感じのもの。
※余談ですが、JIS規格では布系（線維製）の巻尺は10mで4.6mm以内なのに対し、鋼製の巻尺は10mで1.2mm以内でしか誤差が許容されていません。距離を測るときに使う物の材質は本当に大事です。
別の工夫として、人手が足りているなら点A、点B、点Cの3箇所に1人ずつ立って行うことも可能です。この場合はメジャー以外の道具がほぼ不要になるのがメリット。あっても損はないですけど。
点Aや点Bの人は動く必要がないので、DIYならお手伝いをするお子さんでもOK。先に点Aや点Bを決めたら「ここの目印に合わせて動かさないで持っててね」とお願いするだけ。数字を読んだり移動したりするのは点C（仮）の自分だけで良いですからね。（お子さんが本当にじっとしていてくれるかは気にしないこととします）
もし不安なら仮ではない点Cを取り終わってからもう一度全部順番に測って確認すればOKです。
３・４・５である必然性はないので自分でアレンジも可能！
三平方の定理（ピタゴラスの定理）を思い出してもらえばわかりますし、思い出せないのであればもう一度学び直してもらえば気付くと思いますが、３：４：５に拘る必要はありません。
３・４・５は、3^2と4^2を足して数が5^2になっている組み合わせのひとつというだけです。（９＋１６＝２５）
なので、６・８・１０の組み合わせでももちろん出来ます。36+64=100ですから。
基準線にする予定のところの長さが決まっていれば、その数字を使って実寸で計算して直角を出すことすらやろうとすれば可能です。
ただし実際の距離に合わせるとどうしても小数が出てきてしまうので、それを防ぐために３・４・５の組み合わせが使われていたりします。理論上は（距離を測るメジャーが伸びなければ）使う数字が大きいほど直角の精度はよくなるんですけどね。
ちょっと遊んでみるなら、AB間を1m、AC間も1m、BC間を1.41421356（ひとよひとよにひとみごろ）mなんて出し方も出来ます。（私はやりませんし、やったとしても1.414辺りまでしか見ませんけど）
わざわざこんな面倒な数字でやるとすれば、中学生のお子さんと一緒にDIYする場合くらいでしょうか。ちょっとした中学数学のおさらいをしながらという意味を込めて。
さいごに
以上、庭づくりや外構DIYで使える直角の出し方でした。
「ある程度きっちり直角は出したいけど高級機材を買ったりレンタルしてまでやるほどでは……」なんてときに知っておくとサッと使えて便利です。
人手が3人分とメジャーが2つあれば本当に一瞬で出来てしまいますしね。一般的なメジャーは5.5mまでなので３・４・５が個人的には一番楽だと思っています。（安物だと5.5mと書いてあっても5m以上使うたびに寿命が縮むので注意が必要です。そのうち戻らなくなります。）
そこまで厳密に出す必要がなくても、お子さんに「数学は実生活でも使えるんだよ」と教えるために一緒にやってみるのもアリかもしれません。あまり押し付けると逆効果なので難しいところですが。
何かのお役に立てれば幸いです。
